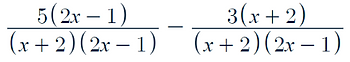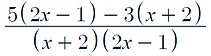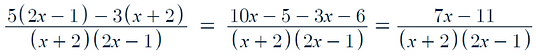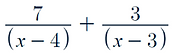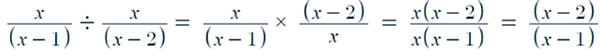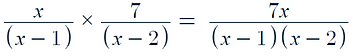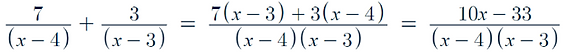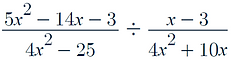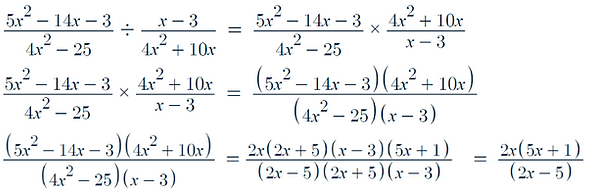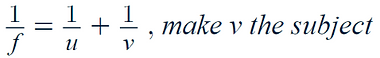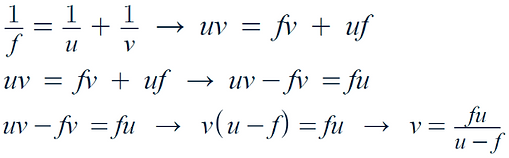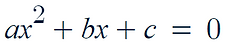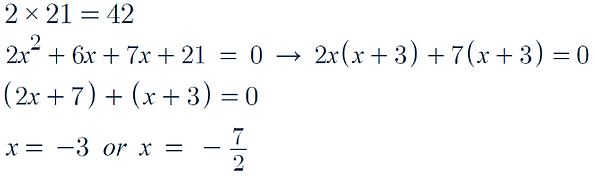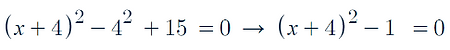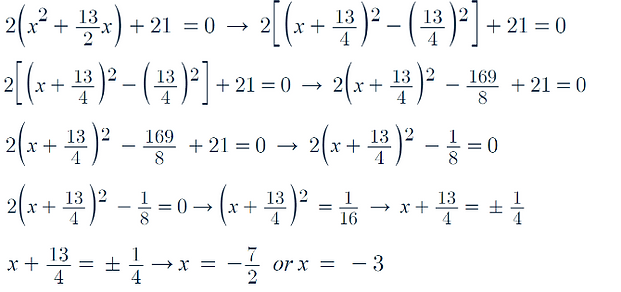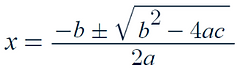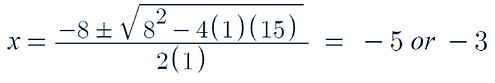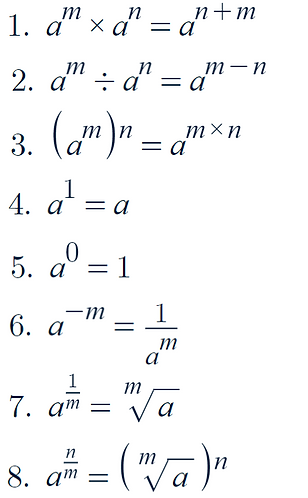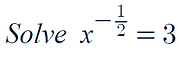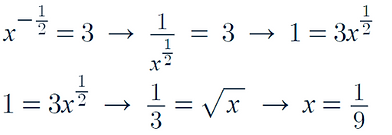FM Algebra | Further Maths

Overview:

Manipulation of rational expressions
Manipulation of formula expressions
Factor Theorem
Quadratic Equations
Inequalities
Index Laws

Adding and Subtracting Rational Expressions

In order to add or subtract rational expressions we must first make the denominators of each fraction the same
Let's take this expression:

In order to make the denominators the same, we have to multiply them together
As we have multiplied each fraction by the denominator of the other, in order for them to remain the same we must add the denominators to the to like so:

Now we can combine our fractions:

Now we just expand out brackets and simplify where possible:

Here we can see that there is no possible simplification, and therefore this is our final answer

Practice Question:

Solution:

Multiplying and Dividing Rational Expressions

In order to multiply rational functions you just have to multiply the numerators together and the denominators together
For example:

In order to divide you must invert the second fraction and now you can just multiply them together
For example:

Practice Question:

Solution:

Manipulation of Formula Expressions

This is rearranging equations in order to change the subject of the equation
The subject of the equation is the variable that is being worked out
For example in the equation y = 2x + 1, y is the subject
In order to rearrange the to make a different variable the subject we must use our algebraic rules
Let's take a look at the question:

Here we want of make v the subject
So we start by multiplying by y to get:

Now we minus u in order to make v the subject:

Practice Question:

Solution:

Factor Theorem:

What is the Factor Theorem:

If f(a) = 0, then the remainder is 0, so (x - a) is a factor of f(x)

For example:

From this we know that x = 2 is a solution of f(x) as (x-2) is a factor:
Therefore we find out what f(2) is equal to

As f(2) = 0, we know that (x - 2) is a factor so we finish with a concluding statement

"Therefore, by the factor theorem, as f(2) = 0, then (x – 2) must be a factor of f(x)"

Quadratic Equations:

There are 3 ways to solve quadratic equations:

Factorising
Completing the square
Using the quadratic equation

The general formula for quadratic equations:

Factorising:

Consider the equation:

In order to factorise this we start by finding factors of our c value multiplied by the a value in the quadratic equation
Here this is 1 x 15 = 15
These factors must add to equal 8, which is our b value in the general formula
Here we can see that 5 and 3 are our factors of 15 that add to equal 8
Knowing this we can separate the 8x into 3x + 5x:

Now we can factorise to parts of our equation:

Now we know that (x+3) and (x+5) are factors of our equation:

Therefore our solutions are x = -3 and x = -5

Practice Question:

Solution:

Completing the square:

Let's consider the same example:

In order to complete the square we start be factoring out the a value in the general formula
Here it is just 1
Now we divide our b value by 2 and turn the x2 into an x, and square the whole thing
We then must minus 42 as produce from the quadratic formed, but is not in our original equation

Now we can solve for x

Practice Question:

Solution:

Quadratic Formula:

The quadratic formula equation:

In order to use the quadratic formula all we have to do is plug in the values from our quadratic equation and solve
For example:

All we have to do is plug in 1, 8 and 15 accordingly:

Inequalities:

Solving linear inequalities:

In order to solve linear inequalities we need to treat them as equations
For example:

Here we just rearrange in terms of x

And this is our range of values for x

Solving Quadratic Inequalities:

In order to solve quadratic inequalities we need to rearrange them in terms of 0
For example:

Then we need to factorise:

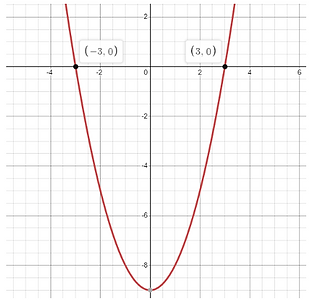
Now we know our solutions are x = 3 and x = -3
Now we can sketch our quadratic graph

As we know that our range of value of x need to be below 0 as (x+3)(x-3) is less than 0, the range of values of x will lie below the y axis
Therefore the range of values of x are -3 < x < 3

Practice Questions:

Solutions:

Index Laws:

Practice Question:

Solution: