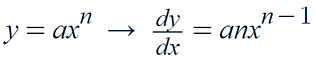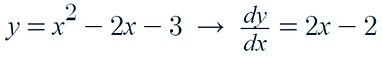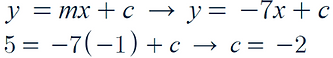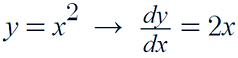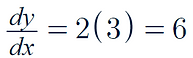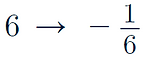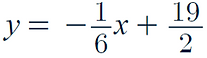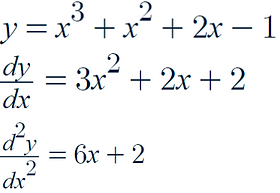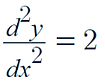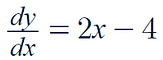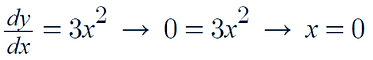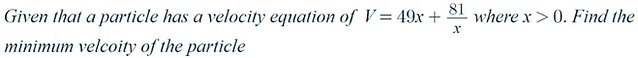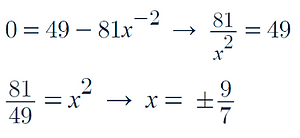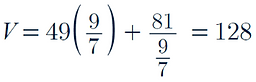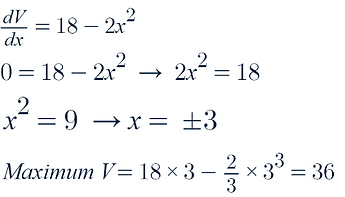Overview 

 

• Gradient Function 

• Tangent and Normal Line of a Curve 

• Second Derivative 

• Minimum and Maximum Points 

• Minimum and Maximum of Problems 

 

 

Gradient Function  

 

 What is the gradient function: 

 

• The gradient function gives the gradient of a curve at a specific point on a curve 

• It is represented as: 

 

​

​

 

Finding the gradient function of a curve: 

 

• In order to find the gradient function we need differentiate the curve equations 

• To do this we multiply the coefficient by the power and minus 1 from the power: 

 

 

​

​

• For example: 

 

 

​

​

 

Practice Questions: 

 

 

1. 

 

 

 

2.​

 

 

 

Solutions: 

​

 

​1.

 

 ​

​

2.

 

 

​

Tangent and Normal Line of a Curve 

 

 

Finding tangent lines to curves: 

 

• Using the gradient function we can the gradient of the any point on a curve 

• This allows gives the gradient of the tangent at this point and we can therefore find the equation of the line 

• Let's consider the question: 

 

 

 

• In order to find the gradient of the tangent at (-1 , 5), we need to find the gradient function: 

 

​

​

​

• Now we need to find the gradient at the point (-1 , 5) 

​

​

​

​

• Therefore the gradient of the tangent is –7 

• Now we can find the equation of the tangent using the point (-1 , 5) and the gradient: 

 

​

​

 

 

• Therefore, the tangent equation is: 

 

 

​

​

Finding the normal lines to curves: 

 

• Here we need to find the gradient at the specific point on a curve 

• Then we need to find the negative reciprocal of the gradient as the normal line is perpendicular to the curve 

 

 

 

• In order to find the gradient of the tangent at (3, 9), we need to find the gradient function: 

​

​

​

​

• Now we need to find the gradient at the point (3 , 9): 

​

​

​

​

• Now we need the negative reciprocal

​

​

​

​

• Therefore the gradient of the tangent is –1/6 

• Now we can find the equation of the tangent using the point (3 , 9) and the gradient: 

 

​

​

​

​

​

 

 

• Therefore, the tangent equation is: 

 

​

​

​

​

 

Second Derivative 

 

What is the second derivative: 

 

• This is a function that measures the rate of change of gradient 

• It is represented as: 

​

​

​

​

​

​

How to find the second derivative of a curve: 

 

• We need to differentiate the curve equation twice 

 

 

​

​

​

​

​

​

​

 

​

​

Practice Question: 

​

​

 

Solutions: 

 

​​

​

​

​

 

​

Minimum and Maximum Points 

 

 

What is a minimum point: 

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

What is a maximum point: 

 

 

 

 

​

​

​

​

​

 

 

 

 

 

 

 

 

What is a point of inflection 

 

 

​

​

​

​

​

​

​

​

​

​

​

​

​

​

 

 

How to find the minimum or maximum points on a graph: 

 

• We need to find the gradient function of the curve  

• Maximum or minimum points are stationary, which is when the gradient is 0 

• So we then let our gradient function equal 0 

• For example: 

 

 

​

​

• We start by finding the gradient function 

 

 

​

​

 

• We then set it equal to zero and solve 

 

​

​

​

• Therefore the x coordinate is 2  

 

 

How can we prove that a stationary point is minimum or maximum or point of inflection: 

 

• We can do this by using the second derivative 

• If the second derivative is greater than 0 then it is a minimum point  

• If the second derivative is equal to 0 then is a point of inflection 

• If the second derivative is less that 0 then it is a maximum point 

• Consider the curve: 

​

​

​

• Find the stationary point of the graph 

 

 

​

 

 

• Now we need to find the second derivative at x = 0 

​

 

 

​

​

• Therefore as our second derivative equals 0, the nature of the stationary point is that it is a point of inflection 

 

 

Practice Question  

 

​

​

​

​

Solutions: 

 

 

​

​

​

​

​

​

 

 

 

 

Minimum and Maximum of Problems 

 

How to find maximum and minimums of problems: 

 

• This is just the same before but with no graph: 

• For example 

 

 

​

​

​

• We need to start by differentiating this function in terms of V and x: 

​

​

​

​

• As we are looking for minimum velocity we let the rate of change of V equal 0 and solve for x: 

 

 

​

​

​

​

​

 

• As x > 0, we know that x = +9/7 

• We therefore plug in the value of x and find the minimum value of V: 

 

 

​

​

​

Practice Question: 

 

​

​

​

 

Solutions: 

​

​

​

​

​

​

​

​

​

​

​