Overview:
-
Features of functions
-
Composite Functions
-
Inverse Functions
-
Sketching Quadratic Functions
-
Sketching Piecewise Functions
Features of Functions
What is a function:
-
A function is a relation or expression involving one or more variables that gives a results when a value is inputted
-
The notation f(x) is usually used to represent a function
What is the domain of a function:
-
The domain is the set of values that can be plugged into a function
What is the range of a function:
-
The range is the set of values that can be outputted from a function
Composite Functions
What is a composite function:
-
It is the result of two or more functions being combined into one
-
Consider the question:
-
Here we would plug g(x) into f(x) as we can see that f is on the outside, while g(x) is inside f(x):
-
Therefore our answer to fg(x) is 8x – 1
Practice question:
Solution:
Inverse Functions
What is the inverse function:
-
This is a function that is the reverse of another function
-
It is when a function is reflected in the line y = x, causing all the Xs to become Ys and all the Ys to become Xs
-
The inverse function notation is f-1(x)
How to find the inverse function:
-
Let's consider the function:
-
In order to make the inverse we must let f(x) = y:
-
Then we need to rearrange the equation to make x the subject:
-
Then we make the x = f-1(x) and make the y = x:
-
And this is the answer.
Practice Questions:
1.
2.
Solutions:
1.
2.
2.
Sketching Quadratic Functions
How to go about sketching quadratic graphs:
-
Let's consider the graph: x + 5x + 6
-
Initially we can see that the y intersect of the graph is (0,6), as when x = 0, y = 6
-
Now we need to find the roots by letting y = 0 and solving the quadratic
-
This gets us x = -2 or x = -3, so we cross the x axis at (-2,0) and (-3,0)
-
Finally we need to consider the shape of the graph
-
As is +x the curve opens upwards, if it was –x then the curve would open downwards
-
-
This leaves us we the graph:
Practice Questions:
1. Sketch the graph y = x +4x+4
2. Sketch the graph y = x +7x+6
Solutions:
1.
2.
Sketching Piecewise Functions:
What is a piecewise function:
-
This is a function that is made up of multiple different functions over different intervals
How to draw a piecewise function:
-
A piecewise function will be made of multiple graph functions
-
In order to draw it you need to draw the individual intervals one at a time
-
At connect them accordingly
-
For example:
-
First we look at the interval 0 ≤ x < 1 and sketch y = x
-
Then we look at the interval 1 ≤ x < 2 and sketch y = 1, starting from the end of the previous interval
-
And finally we do the same thing for the interval 2 ≤ x ≤ 3 with y = 3 - x

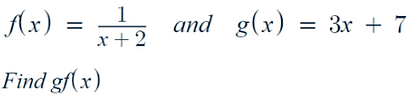




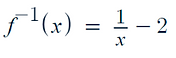


2
2
2






2
2
