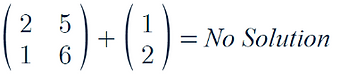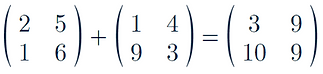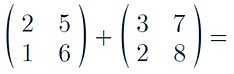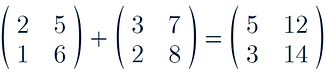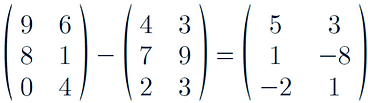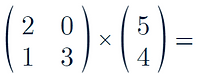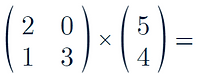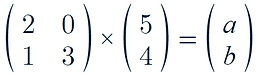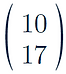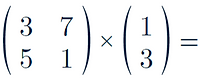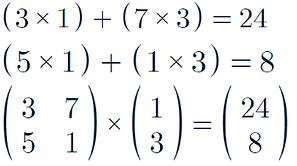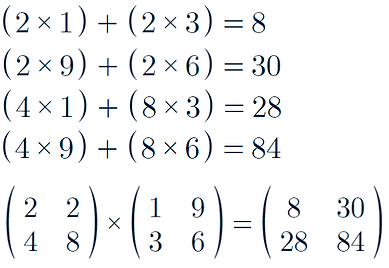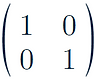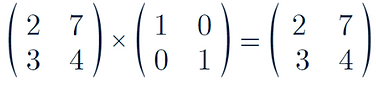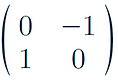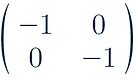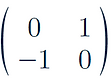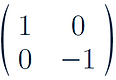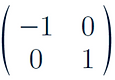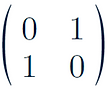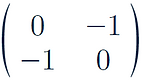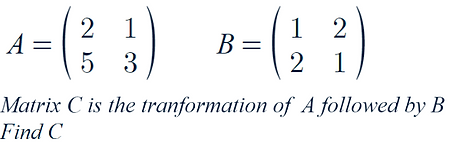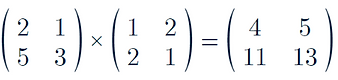Overview
-
Matrix Addition and Subtraction
-
Matrix Multiplication
-
Matrix Transformations
Matrix Addition and Subtraction
How to add matrices together:
-
In order to add matrices together they must have the same dimensions
-
For example:
-
There is no solution as the two matrices have different dimensions
-
However, when they have a same dimensions addition and subtraction is possible
-
In order to add matrices we just add the numbers in each position together
-
For example:
Practice Question:
1.
2.
Solutions :
1.
2.
Matrix Multiplication
How to know if matrix multiplication is possible:
-
We need to look at the dimensions of both matrices
-
If the number of columns on one matrix is equal to the rows of the other then multiplication is possible:
-
Here our first matrix is a 2x2 and the second matrix is a 2x1
-
As the number of columns on the first matrix is 2 and the number of rows on the second matrix is 2, then multiplication is possible
How to find what the dimensions the new matrix is:
-
To find out the dimensions of the new matrix we need to look at the rows of the first matrix and the columns of the second:
-
Here the first matrix has 2 rows and the second matrix has 1 column
-
Therefore the matrix formed is a 2x1 matrix
How to multiply matrices:
-
Once we know the dimensions of the new matrix we have consider each number in the matrix
-
For example:
-
For a we need to multiply the top row of the first matrix by the column in the second matrix
-
For be we need to do the same but with the bottom row of the first matrix
-
Therefore the answer is
Practice Questions:
1.
2.
Solutions:
1.
2.
Matrix Transformations
The identity matrix:
-
Multiplying by it has no effect
Different Types of transformation matrices:
-
Rotation 90 degrees anticlockwise around origin:
-
Rotation 180 degrees anticlockwise around origin:
-
Rotation 270 degrees anticlockwise around origin:
-
Reflections in line x = 0:
-
Reflection in line y = 0:
-
Reflection in line y = x:
-
Reflection in line y = -x:
Combining Matrices:
-
If a point is transformed by matrix A followed by matrix B, we are able to combine these transformations to be represented by 1 matrix
-
This matrix is equal to BA
-
For example:
-
Here we must do B x A in order to find C
-
Hence this is the answer
Practice Question:
Solution: